| Attention | Topic was automatically imported from the old Question2Answer platform. | |
| Asked By | Arseniy |
I struggle do understand how linear interpolation works in the marching square rendering algorithm context.
I created simple example of random floating metaballs to demonstrate the problem:
extends Node2D
class Blob:
var pos_x
var pos_y
var radius
var velocity
func _init(x, y, r, v):
pos_x = x
pos_y = y
radius = r
velocity = v
# Declare member variables here. Examples:
# const a = 2
# var b = "text"
const cell_size = 16
const blobs_count = 10
const blob_size = [20, 40]
const max_sum = 1
var screen_size
var blobs
var allowUpdate = true
const drawMap = {
0: null,
1: [-0.5, 0, 0, -0.5],
2: [-0.5, -1, 0, -0.5],
3: [-0.5, 0, -0.5, -1],
4: [-1, -0.5, -0.5, -1],
5: [-1, -0.5, -0.5, 0, -0.5, -1, 0, -0.5],
6: [-1, -0.5, 0, -0.5],
7: [-1, -0.5, -0.5, 0],
8: [-1, -0.5, -0.5, 0],
9: [-1, -0.5, 0, -0.5],
10: [-1, -0.5, -0.5, -1, -0.5, 0, 0, -0.5],
11: [-1, -0.5, -0.5, -1],
12: [-0.5, -1, -0.5, 0],
13: [-0.5, -1, 0, -0.5],
14: [-0.5, 0, 0, -0.5],
15: null
}
func calcIsoSurface(x1, x2, y1, y2, r):
var dx = x1 - x2
var dy = y1 - y2
var sd = dx*dx + dy*dy
var res = r*r / sd
return res
# Called when the node enters the scene tree for the first time.
func _ready():
screen_size = get_viewport().size
blobs = Array()
var rng = RandomNumberGenerator.new()
var r = rng.randi_range(blob_size[0], blob_size[1])
var x = rng.randi_range(r, screen_size.x - r)
var y = rng.randi_range(r, screen_size.y - r)
for n in range(blobs_count):
blobs.push_back(
Blob.new(
x,
y,
r,
Vector2(rng.randf_range(-1, 1), rng.randf_range(-1, 1))
)
)
print(screen_size)
func formDrawIndex(x, y, sum, vertexes):
var drawIndex = 0
var corners = []
if x > 0 && y > 0:
if sum >= 1:
drawIndex |= 1
corners.push_back(sum)
if vertexes.back() >= 1:
drawIndex |= 2
corners.push_back(vertexes.back())
corners.push_back(vertexes.pop_front())
if corners.back() >= 1:
drawIndex |= 4
if vertexes.front() >= 1:
drawIndex |= 8
corners.push_back(vertexes.front())
return {"draw_index": drawIndex, "corners": corners}
func exLerp(oneSum, zeroSum):
if oneSum == zeroSum:
return null
return (1 - oneSum) / (zeroSum - oneSum)
func interpolateLines(lines, corners):
if lines == null:
return lines
for i in range(0, lines.size(), 2):
var x = lines[i]
var y = lines[i+1]
#somehow implement correct interpolation here
return lines
func drawLines(x, y, lines):
if lines != null && lines.size() >= 4:
draw_line(
Vector2(x + (cell_size*lines[0]), y + (cell_size*lines[1])),
Vector2(x + (cell_size*lines[2]), y + (cell_size*lines[3])),
Color.green
)
if lines != null && lines.size() == 8:
draw_line(
Vector2(x + (cell_size*lines[4]), y + (cell_size*lines[5])),
Vector2(x + (cell_size*lines[6]), y + (cell_size*lines[7])),
Color.green
)
# Called after update() in the _process()
func _draw():
var vertexes = []
for x in range(0, screen_size.x, cell_size):
for y in range(0, screen_size.y, cell_size):
var sum = 0
for blob in blobs:
sum += calcIsoSurface(x, blob.pos_x, y, blob.pos_y, blob.radius)
#draw_circle(Vector2(blob.pos_x,blob.pos_y), blob.radius, Color.darkgray)
#if sum >= 1:
#draw_rect(Rect2(x, y, 1, 1), Color.red)
#else: draw_rect(Rect2(x, y, 1, 1), Color.black)
var indexies = formDrawIndex(x, y, sum, vertexes)
var lines = drawMap[indexies["draw_index"]]
lines = interpolateLines(lines, indexies["corners"])
drawLines(x, y, lines)
vertexes.push_back(sum)
if x > 0:
vertexes.pop_front()
func _input(event):
if event is InputEventMouseButton && event.is_pressed():
allowUpdate = !allowUpdate
print(allowUpdate)
# Called every frame. 'delta' is the elapsed time since the previous frame.
func _process(delta):
if !allowUpdate:
return
update()
for blob in blobs:
blob.pos_x += blob.velocity.x
blob.pos_y += blob.velocity.y
if blob.pos_x > screen_size.x || blob.pos_x < 0:
blob.velocity.x *= -1
if blob.pos_y > screen_size.y || blob.pos_y < 0:
blob.velocity.y *= -1
The outcome looks something like this:
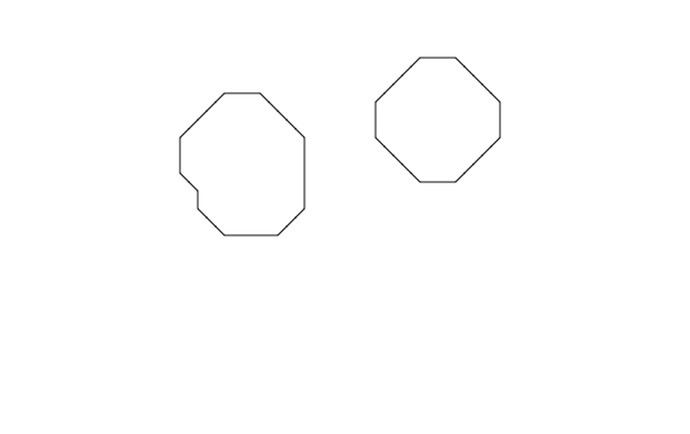
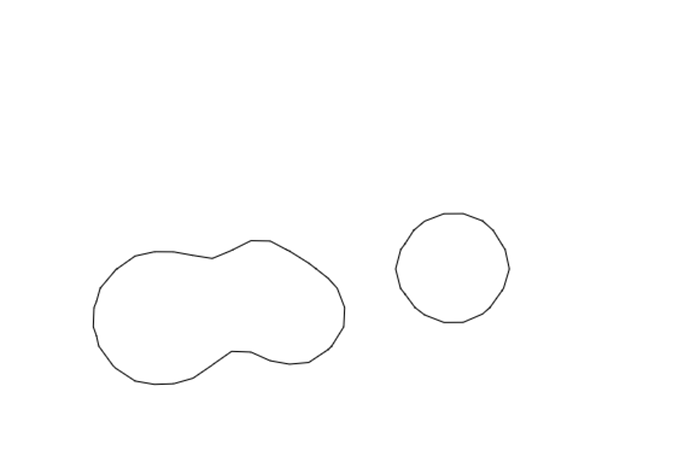
Now I would like to apply linear interpolation to make my meatballs smoother. This is where I stuck. The desire outcome is transform rendering of this:
To this:
I already created interpolateLines and exLerp functions, but don’t understand how exactly in this context linear interpolation works and why? I used this material as a theory for code implementation, but last part is still blurry for me.
Anyone can provide working code example and explain theory in dump language with more deep math explanation and visual demonstration? So I can finally breakthrough this problem.