|
|
|
 |
Reply From: |
njamster |
If it calculates the distance between two vectors, why does it [need] a direction?
A vector is a direction. The starting point is always assumed to be in the origin point - i.e. Vector2(0, 0) - pointing towards (in your case) the global_position.
Also angle_to does not calculate the distance between two vectors, that’s what (to no surprise) distance_to does! It does (as the name suggests) calculate the angle phi between two vectors a and b, both originating from the origin at (0, 0):
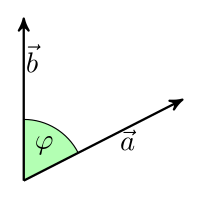
So, yes, if the Player node moves towards the other node the angle will shrink and eventually reach zero, as their global_position-vectors become identical. Nothing wrong about that. Cannot imagine a reason why it shouldn’t be able to become bigger than 30° however. In fact, for me it does (using the first code snippet you shared). So your problem likely is related to something else, as your script is correct.
However, your second code snippet doesn’t make sense. You’re creating a unit vector pointing upwards and rotate this by the global_rotation of your node. A rotation of 0° defaults to a vector pointing right though, not up. So if the node would be facing upwards, your direction-vector would point to the left. Other than that it’s the same code, so you will get the angle (in degrees) between that vector pointing left and the vector pointing to your player. Don’t really get what you were trying to do here.
One reason the angle never gets bigger in the first code might be that the global origin is far away.
Kaligule | 2020-02-15 15:21
Thank you so much! That does help a lot.
So just that I get it right: angle_to measures the angle phi between the two vectors and that angle is positioned at the top left (0,0)?
What I wanted to do was to get the angle between the two vectors with the angle being at the at the vector (as opposed to the top left). angle_to_point solved that well. Sorry, should have been more precise.
Any chance you know a good tutorial for vectors? I read the one from the godot documentation and the gdquest videos; but I still feel wobbly on it.
1izNoob | 2020-02-16 10:52
I’m not sure what you mean by “top left”, but let’s try with an example:
var a = Vector2.RIGHT # Vector2(1, 0)
var b = Vector2.UP # Vector2(0, 1)
print(rad2deg(a.angle_to(b))) # will print -90
print(rad2deg(b.angle_to(a))) # will print 90
Again: In Godot a rotation of 0° defaults to a vector pointing right. Rotating clockwise is considered the norm, so if you want to rotate counter-clockwise, you’d have to add a minus in front. That’s why the angle from a to b is negative, but the angle from b to a isn’t. Also note, that these angles won’t become bigger than 180°. Because if you would get b through rotating a by 181°, you could also rotate a by -179° instead.
With angle_to_point you use a and b to describe a third vector between them and then calculate the angle between this vector and the x-axis (pointing right):
var x_axis = Vector2.RIGHT
var a_to_b = a - b
print(rad2deg(x_axis.angle_to(a_to_b))) # will print 45
print(rad2deg(a.angle_to_point(b))) # will print 45
var b_to_a = b - a
print(rad2deg(x_axis.angle_to(b_to_a))) # will print -135
print(rad2deg(b.angle_to_point(a))) # will print -135
Note that the orientation of a vector matters, so a.angle_to_point(b) is not the same as b.angle_to_point(a). The former will calculate the angle between the x-axis and a vector pointing to the bottom right (hence 45°), the latter will calculate the angle between the x-axis and a vector pointing to the top left (hence -135°).
In terms of math tutorials, I cannot recommend 3Blue1Brown enough!
njamster | 2020-02-16 13:44
