|
|
|
 |
Reply From: |
Dlean Jeans |
Adapted from https://gist.github.com/shaunlebron/8832585:
func lerp_angle(from, to, weight):
return from + short_angle_dist(from, to) * weight
func short_angle_dist(from, to):
var max_angle = PI * 2
var difference = fmod(to - from, max_angle)
return fmod(2 * difference, max_angle) - difference
Thank you very much! Here’s the final code for the people from the future:
extends Sprite
var direction:Vector2
var smooth:float = 5.0
func _process(delta):
if Input.is_action_pressed("ui_left"):
direction.x = -1
if Input.is_action_pressed("ui_right"):
direction.x = 1
if Input.is_action_pressed("ui_up"):
direction.y = 1
if Input.is_action_pressed("ui_down"):
direction.y = -1
```
direction = direction.normalized()
var facing:float = atan2(direction.x, direction.y)
rotation = lerp_angle(rotation, facing, smooth * delta)
```
func lerp_angle(from, to, weight):
return from + short_angle_dist(from, to) * weight
func short_angle_dist(from, to):
var max_angle = PI * 2
var difference = fmod(to - from, max_angle)
return fmod(2 * difference, max_angle) - difference
librepyxel | 2019-02-22 10:16
Glad it helps! 
Dlean Jeans | 2019-02-22 15:49
Hi,
your solution works well for me … almost.
Maybe you or someone else can help me?
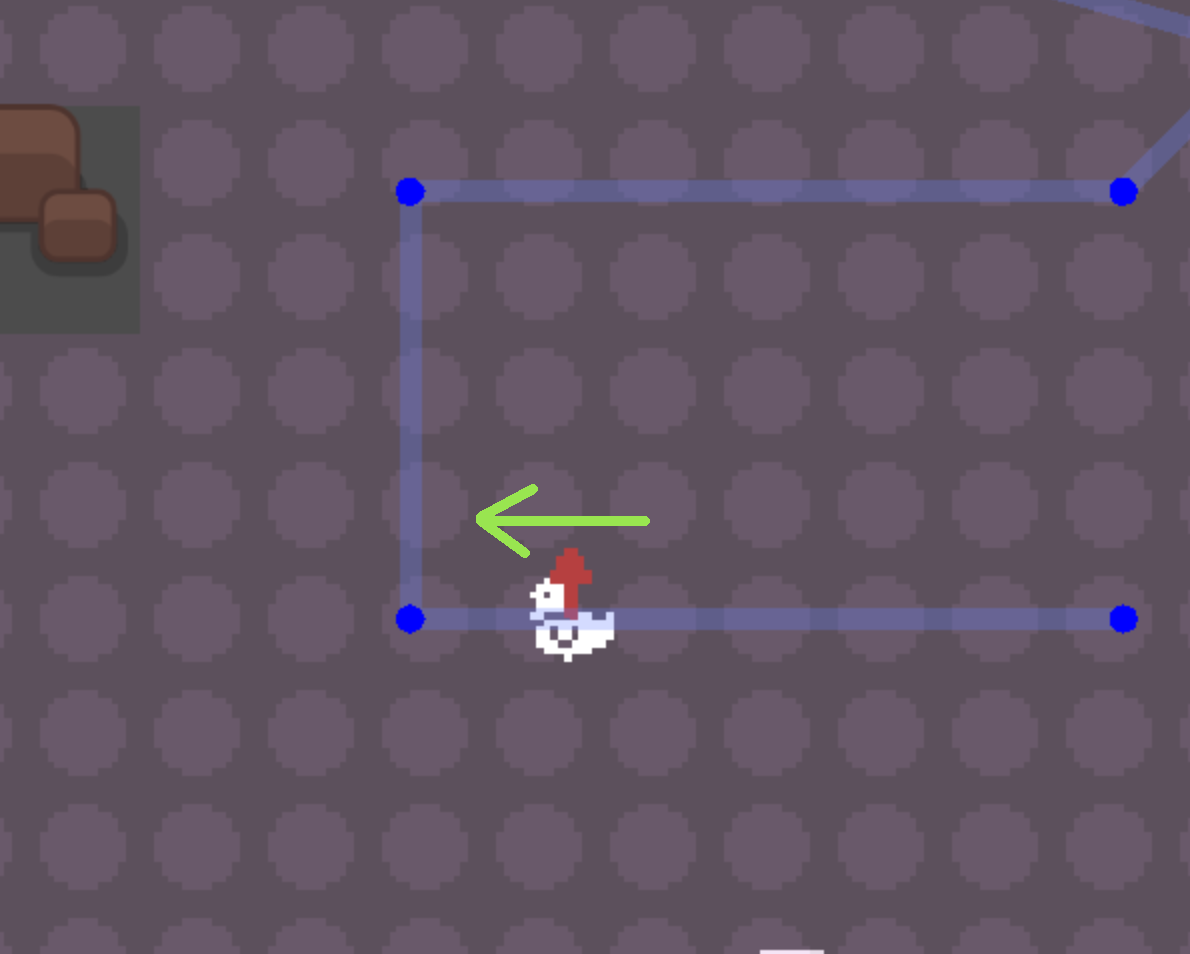
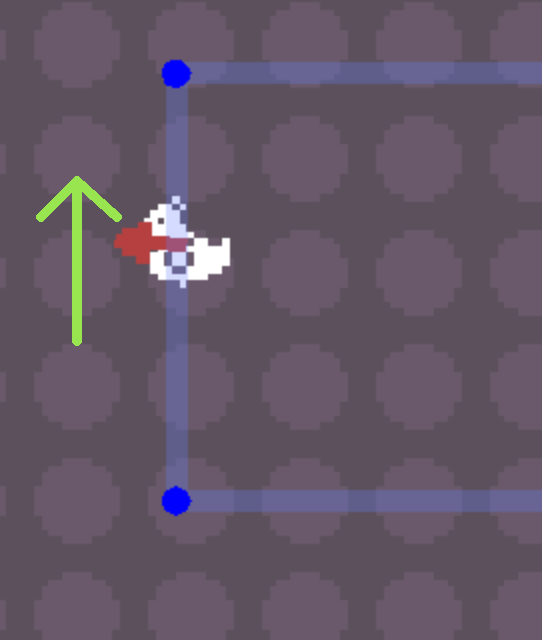
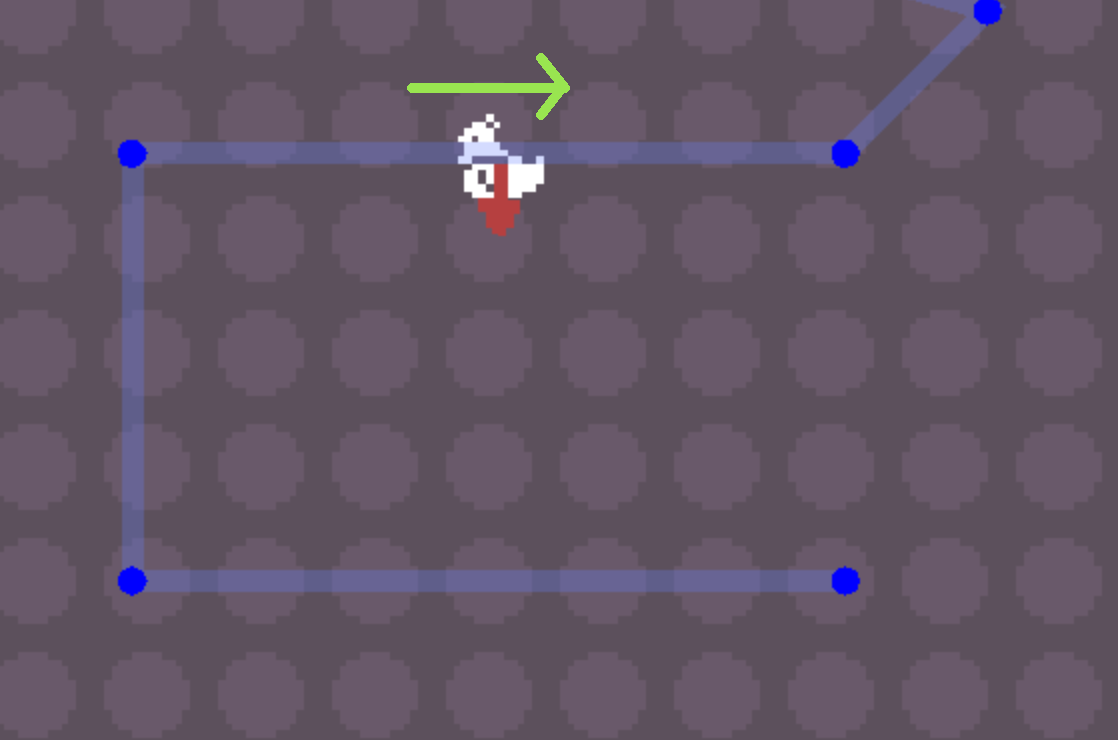
In my scene I have a chicken and a red arrow as an additional sprite node pointing to the right, rotation of the this arrow is 0 by default.
If I apply your code the following happens:
The direction vector of the chicken (green arrow) is pointing to the left, but the arrow rotates upwards.
When the direction vector is pointing upwards the arrow is pointing to the left, and when the chicken is moving to the right the arrow is moving down.
I’m working on this rotation issue since weeks (not jocking! - I’ve learned a lot about trigonometry) and still I don’t find a solution and I’m not 100% able to understand your code 
Could pls anybody give me a hint?
Thanks, Boris
boris0dev | 2019-08-27 17:32
I think I solved it on my own!
I converted the angle the atan2 returns (which is a trigonometry angle = left handed) to a godot angle (=right handed) with the following modification:
func _process(delta):
direction = <any vector>
direction = direction.normalized()
var facing:float = atan2(direction.x, direction.y)
var godot_facing = trigonometry_angle_to_godot_angle(facing)
rotation = lerp_angle(rotation, godot_facing, smooth * delta)
func lerp_angle(from, to, weight):
return from + short_angle_dist(from, to) * weight
func short_angle_dist(from, to):
var max_angle = PI * 2
var difference = fmod(to - from, max_angle)
return fmod(2 * difference, max_angle) - difference
func trigonometry_angle_to_godot_angle(angle_radians):
return -angle_radians + deg2rad(90)
The only issue I am having now that the whole movement is somehow stuttering…
And still I don’t understand what “short_angle_dist()” is exactly doing, though I try to calculate the values with a calculator…
boris0dev | 2019-08-27 18:07
Update: The code of Dlean Jeans has a small but significant error: you have to swap the arguments for atan2:
Wrong:
direction = direction.normalized()
var facing:float = atan2(direction.x, direction.y)
rotation = lerp_angle(rotation, facing, smooth * delta)
Correct:
direction = direction.normalized()
var facing:float = atan2(direction.y, direction.x)
rotation = lerp_angle(rotation, facing, smooth * delta)
This way my complicated transformation from trigonometry angle to a godot angle isn’t necessary 
boris0dev | 2019-08-28 13:32