I somewhat understand your problem.
I understand that you want to create a system that moves a node on a path from A to B. The speed of the node should be configurable and should be accelerated from/to 0 near the start and end of the path.
Is it right to assume that time is not important here; it doesn’t matter how long it takes for the node to reach its destination?
Let me know whether if what I just described is correct.
Movement with eased acceleration
To produce a system that is capable of starting and stopping a node between two points, you have to know some information:
- Distance to B
- Stopping distance of easing function (relative to the max speed)
- Acceleration distance of easing function (relative to the max speed)
To elaborate, the distance to B must be known so the node knows when to start “braking”. The crucial part of this system is, as you pointed out, knowing when to stop the node.
By using a (easing) function to define the speed of an object, we can use calculus to compute the distance that the object of that speed travels.
Using calculus to compute travel distance
Before describing how we can use calculus to compute the travel distance, it is worth explaining why we can do so in the first place.
It is trivially known in physics that the distance an object travels over a period of time is:
distance_travelled = speed[m/s] * time[s]
The presupposition here is that speed and time are constant. In your case, they are not – delta and speed varies over time. So how do we compute the distance travelled? The answer is to slice up time into discrete chunks and sum up these chunks to approximate the travel distance. For physics simulations (such as those seen in games), these chunks are often large so the game can run in real-time, but in mathematics we can slice up time into infinitely many chunks and arrive at the exact solution.
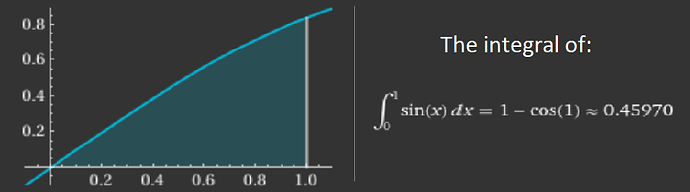
While being a rather crude description, an integral in calculus is essentially that – slicing up a function into infinitely many pieces in order to compute the area defined by a function and an upper and lower bound.
The area under the function, sin(x), within the bounds of [0, 1] is seen in blue.
Let us now use a function that is more applicable to your use case.
Easing function: sin(x * PI / 2) * speed
speed = 10.0
As seen in the image above, the travel distance for sin(x) with a speed of 10.0 is 6.3662.
Translating the math into usable code
We have now learned how to compute the travel distance of an easing function, and we can now use this distance as a threshold so we know when to start tweening.
However, I imagine you would want to configure the system on the fly without heading to some third-party math website (Wolfram Alpha) every time you want to use a different function or different values. Unfortunately, GDScript (and most other languages as far as I know) do not offer a simple integral() function. You will have to make your own. Without going into too much detail, I have added my attempt at an integral() function below that uses the principle of “time slicing” previously outlined.
# Takes the integral of a Curve instance with the specified step size and bounds.
func integral(custom_function: Curve, lower_bound, upper_bound, step_size) -> float:
var value_range = upper_bound - lower_bound
var steps_in_range = value_range / step_size # Slices in the value range
var result = 0
for i in range(steps_in_range):
var x = lower_bound + step_size * i # The input value
var y = custom_function.evaluate(x) # The output value
var area = y * step_size # The slice area
result += area
return result
Context-dependent invocation example:
var easing_function: Curve
var distance_travelled = integral(easing_function, 0, 1, 100)
Performing the movement
I think you got this part down already but just to be complete, I’ll provide some code that uses the distance_travelled to start and stop a node on a path between two points as originally described.
This code example is not done yet and contains missing lines of code and errors. I was too tired to go on. It will be corrected ASAP.
@export var node_A: Node2D
@export var node_B: Node2D
@export var easing_function: Tween.TransitionType
@export var max_speed = 1
var speed = 0
var node: Node2D # The node that moves
var start_moving = false
enum MoveState { STARTING, MOVING, STOPPING, STOPPED }
var current_state = MoveState.STOPPED
var current_tween: Tween
func _process(delta):
var toB = node_B.global_position - node.global_position
var distance = toB.length()
var direction = toB.normalized()
# TODO: Find a good way to match transtion types with functions for use with integral().
var stopping_distance = integral(###, ###, ###, ###)
if distance <= stopping_distance && current_state == MoveState.MOVING:
stop()
func start():
if current_tween:
current_tween.kill()
current_tween = create_tween()
current_tween.tween_property(self, speed, max_speed, 1).set_trans(easing_function)
current_state = MoveState.STARTING
current_tween.finished.connect(func(): current_state = MoveState.MOVING)
func stop():
if current_tween:
current_tween.kill()
current_tween = create_tween()
current_tween.tween_property(self, speed, 0, 1).set_trans(easing_function)
current_state = MoveState.STOPPING
current_tween.finished.connect(func(): current_state = MoveState.STOPPED)
This code example is not done yet and contains missing lines of code and errors. I was too tired to go on. It will be corrected ASAP.
I hope this helps you achieve what I think you’re going for. It’s a lot easier to move an object with easing functions if the speed can be arbitrary, but since your goal is constant speed “mid-flight” I think this might be a good approach.
Let me know if anything needs correction – I hardly use GDScript so I’ve been reading the docs quite a bit.