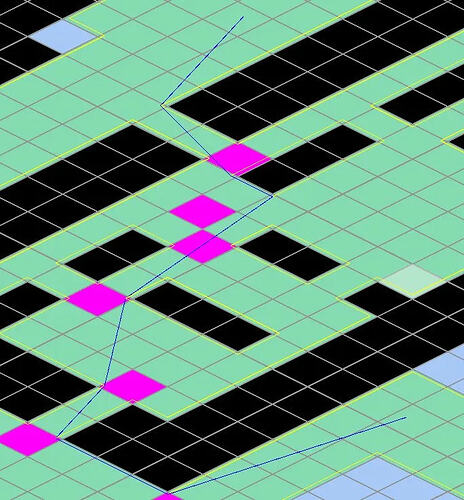
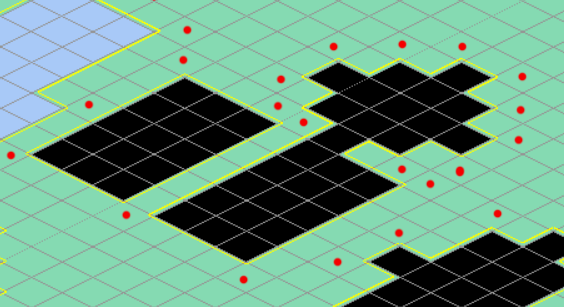
I figured I’d include my code for anyone willing to dig in. Here’s the relevant files:
- pathfinder.gd: The meat of it. A* search, tile-level path smoothing, and
cast_ray() against the boundary polygons. This is where the snap-to-corner logic would need to live.
- grid.gd: Map data, obstacle cluster detection (flood fill), boundary polygon tracing with margins, Bresenham line-of-sight, and coordinate conversions between grid space and world space.
- fixed_geometry.gd: Integer-only segment intersection. Returns t values as numerator/denominator to avoid any division.
- fixed_vec2.gd: Deterministic 2D vector using scaled integers (SCALE=1000). Every simulation position uses this.
- intersection_result.gd: Data class for segment intersection results — t value as a fraction + the intersection point.
- raycast_result.gd: Data class for
cast_ray() results — wraps an intersection result plus which boundary and edge got hit.
pathfinder.gd
## A* pathfinder operating on the game grid.
## Uses Chebyshev distance as heuristic for diagonal movement,
## where straight steps cost 1000 and diagonal steps cost 1414 (√2 × 1000).
## All costs use integer math for determinism.
class_name Pathfinder
extends RefCounted
## Cost for moving to an adjacent tile (straight).
const STRAIGHT_COST: int = 1000
## Cost for moving to a diagonal tile (√2 × 1000, approximated).
const DIAGONAL_COST: int = 1414
## The grid to pathfind on.
var grid: Grid
func _init(grid_ref: Grid) -> void:
grid = grid_ref
#region A* Pathfinding
## Finds the shortest path between two walkable tiles using A*.
## Returns an ordered array of tile coordinates from start to end,
## excluding the start tile. Returns empty if no valid path exists.
func find_path(start: Vector2i, end: Vector2i) -> Array[Vector2i]:
if start == end: return []
var start_tile: Tile = grid.get_tile(start.x, start.y)
var end_tile: Tile = grid.get_tile(end.x, end.y)
if start_tile == null or not start_tile.is_walkable(): return []
if end_tile == null or not end_tile.is_walkable(): return []
var closed_set: Dictionary[Vector2i, bool] = {}
var came_from: Dictionary[Vector2i, Vector2i] = {}
var g_score: Dictionary[Vector2i, int] = {}
var open_queue: Array = []
g_score[start] = 0
_insert_into_queue(open_queue, start, _heuristic(start, end))
while open_queue.size() > 0:
var current: Vector2i = open_queue.pop_front()[1]
if closed_set.has(current):
continue
if current == end:
return _retrace_path(came_from, end)
closed_set[current] = true
for neighbour: Vector2i in grid.get_neighbours(current.x, current.y):
if closed_set.has(neighbour):
continue
var tile: Tile = grid.get_tile(neighbour.x, neighbour.y)
if not tile.is_walkable():
continue
# Block diagonal movement if either adjacent cardinal tile is unwalkable.
# Prevents units squeezing between diagonally-touching obstacles.
var dx: int = neighbour.x - current.x
var dy: int = neighbour.y - current.y
if dx != 0 and dy != 0:
var cardinal_a: Tile = grid.get_tile(current.x + dx, current.y)
var cardinal_b: Tile = grid.get_tile(current.x, current.y + dy)
if cardinal_a == null or not cardinal_a.is_walkable() or cardinal_b == null or not cardinal_b.is_walkable():
continue
var tentative_g: int = g_score[current] + _get_move_cost(current, neighbour)
if not g_score.has(neighbour) or tentative_g < g_score[neighbour]:
g_score[neighbour] = tentative_g
came_from[neighbour] = current
var f: int = tentative_g + _heuristic(neighbour, end)
_insert_into_queue(open_queue, neighbour, f)
return []
## Inserts a tile into the sorted open queue using binary search.
func _insert_into_queue(queue: Array, tile: Vector2i, f_score: int) -> void:
var low: int = 0
var high: int = queue.size()
while low < high:
@warning_ignore("integer_division")
var mid: int = (low + high) / 2
if queue[mid][0] < f_score:
low = mid + 1
else:
high = mid
queue.insert(low, [f_score, tile])
## Estimates the cost from one tile to another using Chebyshev distance.
func _heuristic(from: Vector2i, to: Vector2i) -> int:
var dx: int = abs(from.x - to.x)
var dy: int = abs(from.y - to.y)
var diagonal: int = mini(dx, dy)
var straight: int = abs(dx - dy)
return diagonal * DIAGONAL_COST + straight * STRAIGHT_COST
## Returns the movement cost between two adjacent tiles.
func _get_move_cost(current: Vector2i, neighbour: Vector2i) -> int:
var diff: int = abs(current.x - neighbour.x) + abs(current.y - neighbour.y)
if diff == 2:
return DIAGONAL_COST
return STRAIGHT_COST
## Retraces the path from end to start using the came_from map.
## Returns the path in order from start to end, excluding the start tile.
func _retrace_path(came_from: Dictionary[Vector2i, Vector2i], end: Vector2i) -> Array[Vector2i]:
var path: Array[Vector2i] = []
var current: Vector2i = end
while came_from.has(current):
path.append(current)
current = came_from[current]
path.reverse()
return path
#endregion
#region Path Smoothing
## Removes redundant waypoints by brute-force: tries to skip each intermediate
## point and keeps it only if the shortcut crosses unwalkable terrain.
func smooth_path(start: Vector2i, path: Array[Vector2i]) -> Array[Vector2i]:
if path.is_empty():
return []
var points: Array[Vector2i] = [start]
points.append_array(path)
var i: int = 0
while i < points.size() - 2:
if grid.has_line_of_sight(points[i], points[i + 2]):
points.remove_at(i + 1)
else:
i += 1
points.remove_at(0)
return points
## Converts grid-space waypoints to world-space positions for unit movement.
func to_world_path(path: Array[Vector2i]) -> Array[FixedVec2]:
var result: Array[FixedVec2] = []
for point: Vector2i in path:
result.append(grid.grid_to_world(point.x, point.y))
return result
#endregion
#region Raycasting
## Casts a ray from one point to another and finds the closest boundary edge it hits.
## Returns a RaycastResult with the hit details, or null if the ray reaches its
## destination without crossing any obstacle boundary.
func cast_ray(from: FixedVec2, to: FixedVec2) -> RaycastResult:
var closest_hit: RaycastResult = null
for boundary_index in grid.obstacle_boundaries.size():
var boundary: Array = grid.obstacle_boundaries[boundary_index]
for edge_index in boundary.size():
var edge_start: Vector2i = boundary[edge_index]
var edge_end: Vector2i = boundary[(edge_index + 1) % boundary.size()]
var result: IntersectionResult = FixedGeometry.segment_intersect(
from, to,
FixedVec2.from_raw(edge_start.x, edge_start.y),
FixedVec2.from_raw(edge_end.x, edge_end.y)
)
if result == null:
continue
# First hit, or closer than the current closest. Compare t values
# by cross-multiplying to avoid division.
if closest_hit == null or result.t_numerator * closest_hit.intersection.t_denominator < closest_hit.intersection.t_numerator * result.t_denominator:
closest_hit = RaycastResult.new(result, boundary_index, edge_index)
return closest_hit
#endregion
grid.gd
## 2D grid of tiles representing the game map.
## Stores terrain data and provides coordinate conversion
## between world space (FixedVec2) and grid space (integers).
class_name Grid
extends RefCounted
## Boundary polygons for each obstacle cluster, with margin offset applied.
## Each element is an Array[Vector2i] of raw fixed-point corner positions.
@warning_ignore("integer_division")
const OBSTACLE_MARGIN: int = FixedPoint.SCALE / 10
## Direction index for rightward movement in corner space.
const DIR_RIGHT: int = 0
## Direction index for downward movement in corner space.
const DIR_DOWN: int = 1
## Direction index for leftward movement in corner space.
const DIR_LEFT: int = 2
## Direction index for upward movement in corner space.
const DIR_UP: int = 3
## Horizontal movement delta per direction in corner space.
const DIR_DX: Array[int] = [1, 0, -1, 0]
## Vertical movement delta per direction in corner space.
const DIR_DY: Array[int] = [0, 1, 0, -1]
## Obstacle tile column offset relative to corner, per clockwise (CW) travel direction.
const CW_OBS_DX: Array[int] = [0, -1, -1, 0]
## Obstacle tile row offset relative to corner, per clockwise (CW) travel direction.
const CW_OBS_DY: Array[int] = [0, 0, -1, -1]
## Walkable tile column offset relative to corner, per clockwise (CW) travel direction.
const CW_WALK_DX: Array[int] = [0, 0, -1, -1]
## Walkable tile row offset relative to corner, per clockwise (CW) travel direction.
const CW_WALK_DY: Array[int] = [-1, 0, 0, -1]
## Outward-facing normal X component per direction, used for margin offset.
const NORMAL_DX: Array[int] = [0, 1, 0, -1]
## Outward-facing normal Y component per direction, used for margin offset.
const NORMAL_DY: Array[int] = [-1, 0, 1, 0]
## Width of the map in tiles.
var map_width: int
## Height of the map in tiles.
var map_height: int
## 2D array of [Tile] objects, accessed as map_data[col][row].
var map_data: Array[Array]
## Groups of connected unwalkable tiles, found by 4-connectivity flood fill.
## Each element is an Array[Vector2i] of tile positions belonging to one cluster.
var obstacle_clusters: Array[Array]
## Maps each unwalkable tile position to its cluster index in obstacle_clusters.
var obstacle_lookup: Dictionary[Vector2i, int]
## Boundary polygons for each obstacle cluster, with margin offset applied.
## Each element is an Array[Vector2i] of raw fixed-point corner positions.
var obstacle_boundaries: Array[Array]
## Initializes the grid with the given dimensions, filled with plains tiles.
func _init(width: int, height: int) -> void:
map_width = width
map_height = height
for n in height:
var row: Array[Tile] = []
for m in width:
row.append(Tile.new(Tile.TerrainType.PLAINS))
map_data.append(row)
## Returns the [Tile] at the given grid coordinates, or null if out of bounds.
func get_tile(col: int, row: int) -> Tile:
if _is_in_bounds(col, row):
return map_data[col][row]
else:
push_warning("Tile out of bounds: (%d, %d)" % [col, row])
return null
## Converts a world position to grid coordinates by flooring.
func world_to_grid(world_position: FixedVec2) -> Vector2i:
@warning_ignore("integer_division")
return Vector2i(world_position.x.value / FixedPoint.SCALE, world_position.y.value / FixedPoint.SCALE)
## Converts grid coordinates to the center of that tile in world space.
func grid_to_world(col: int, row: int) -> FixedVec2:
return FixedVec2.from_fixed_point(
FixedPoint.from_raw(_center_fixed_point(col)),
FixedPoint.from_raw(_center_fixed_point(row))
)
## Returns the raw fixed-point value for the center of a tile along one axis.
func _center_fixed_point(input: int) -> int:
@warning_ignore("integer_division")
return input * FixedPoint.SCALE + FixedPoint.SCALE / 2
## Returns all in-bounds neighbouring tile coordinates, including diagonals.
func get_neighbours(col: int, row: int) -> Array[Vector2i]:
var result: Array[Vector2i] = []
for offset_x in range(-1, 2):
for offset_y in range(-1, 2):
if offset_x == 0 and offset_y == 0:
continue
var neighbour_col: int = col + offset_x
var neighbour_row: int = row + offset_y
if _is_in_bounds(neighbour_col, neighbour_row):
result.append(Vector2i(neighbour_col, neighbour_row))
return result
## Returns all 4 cardinal in-bounds neighbouring tile coordinates.
func get_cardinal_neighbours(col: int, row: int) -> Array[Vector2i]:
var result: Array[Vector2i] = []
# Top neighbour
if _is_in_bounds(col, row -1):
result.append(Vector2i(col, row -1))
# Right neighbour
if _is_in_bounds(col + 1, row):
result.append(Vector2i(col + 1, row))
# Bottom neighbour
if _is_in_bounds(col, row + 1):
result.append(Vector2i(col, row + 1))
# Left neighbour
if _is_in_bounds(col - 1, row):
result.append(Vector2i(col - 1, row))
return result
## Returns true if a Tile is in bounds.
func _is_in_bounds(col: int, row: int) -> bool:
return col >= 0 and col < map_width and row >= 0 and row < map_height
## Creates a [Grid] from a JSON map file at the given path.
## The file must contain "width", "height", and a "tiles" 2D array
## where each value maps to a [Tile.TerrainType] enum value.
## Returns null if the file is missing or fails to parse.
static func from_file(path: String) -> Grid:
if not FileAccess.file_exists(path):
push_warning("Map file not found!")
return
var map_file: FileAccess = FileAccess.open(path, FileAccess.READ)
var parsed_map: JSON = JSON.new()
var content: String = map_file.get_as_text()
var error: int = parsed_map.parse(content)
if error == OK:
var data: Dictionary = parsed_map.data
var grid: Grid = Grid.new(data["width"], data["height"])
for row in data["height"]:
for col in data["width"]:
var tile_type: int = data["tiles"][row][col]
grid.get_tile(col, row).type = tile_type as Tile.TerrainType
grid._build_obstacle_clusters()
return grid
return null
## Checks if a straight line between two tiles passes only through walkable tiles.
## Uses Bresenham's line algorithm. Diagonal steps are blocked if either adjacent
## cardinal tile is unwalkable, matching the movement rules used by A*.
func has_line_of_sight(from: Vector2i, to: Vector2i) -> bool:
var horizontal_distance: int = abs(to.x - from.x)
var vertical_distance: int = abs(to.y - from.y)
var horizontal_step: int = 1 if from.x < to.x else -1
var vertical_step: int = 1 if from.y < to.y else -1
var error: int = horizontal_distance - vertical_distance
var current: Vector2i = from
while current != to:
var tile: Tile = get_tile(current.x, current.y)
if tile == null or not tile.is_walkable():
return false
var double_error: int = error * 2
var step_horizontal: bool = double_error > -vertical_distance
var step_vertical: bool = double_error < horizontal_distance
if step_horizontal and step_vertical:
var cardinal_a: Tile = get_tile(current.x + horizontal_step, current.y)
var cardinal_b: Tile = get_tile(current.x, current.y + vertical_step)
if (cardinal_a == null or not cardinal_a.is_walkable()) or (cardinal_b == null or not cardinal_b.is_walkable()):
return false
if step_horizontal:
error -= vertical_distance
current.x += horizontal_step
if step_vertical:
error += horizontal_distance
current.y += vertical_step
return true
#region Cluster boundaries
## Finds all groups of connected unwalkable tiles using 4-connectivity flood fill,
## then traces the boundary polygon of each group with an outward margin offset.
## Populates obstacle_clusters, obstacle_lookup, and obstacle_boundaries.
func _build_obstacle_clusters() -> void:
var visited: Dictionary[Vector2i, bool] = {}
for row in map_height:
for col in map_width:
var tile: Tile = get_tile(col, row)
var tile_position = Vector2i(col, row)
# Skip tiles we've already assigned to a cluster, or walkable tiles.
if visited.get(tile_position) or tile.is_walkable():
continue
# Found an unvisited unwalkable tile. We will flood fill to find all
# connected unwalkable tiles, forming one cluster.
var cluster: Array[Vector2i] = []
var queue: Array[Vector2i] = [tile_position]
visited.get_or_add(tile_position, true)
while queue.size() > 0:
var first_tile_coords: Vector2i = queue.pop_front()
cluster.append(first_tile_coords)
for neighbour in get_cardinal_neighbours(first_tile_coords.x, first_tile_coords.y):
if visited.get(neighbour) == null and not get_tile(neighbour.x, neighbour.y).is_walkable():
visited.get_or_add(neighbour, true)
queue.append(neighbour)
# Register every tile in this cluster for fast lookup during boundary tracing.
var cluster_index: int = obstacle_clusters.size()
for tile_pos in cluster:
obstacle_lookup[tile_pos] = cluster_index
obstacle_clusters.append(cluster)
print("Obstacle clusters: %d" % obstacle_clusters.size())
# Trace the boundary polygon of each cluster with margin offset applied.
for cluster in obstacle_clusters:
obstacle_boundaries.append_array(_trace_cluster_boundaries(cluster))
## Traces all boundary loops of a cluster by consuming edges from an unvisited set.
## Each loop walks clockwise around the boundary, recording vertices where the
## direction changes with an outward margin offset applied.
## Returns multiple loops: one outer boundary plus any inner boundaries (holes)
## where walkable terrain is enclosed by the cluster.
func _trace_cluster_boundaries(cluster: Array[Vector2i]) -> Array[Array]:
var all_loops: Array[Array] = []
var cluster_index: int = obstacle_lookup[cluster[0]]
var unvisited: Dictionary[Vector3i, bool] = _get_cluster_boundary_edges(cluster, cluster_index)
while not unvisited.is_empty():
# Pick any edge as start
var start: Vector3i = unvisited.keys()[0]
# Walk the boundary from the starting edge, corner by corner. Decides new
# direction at each corner, in order: Right, straight, left, U-turn.
# A direction is valid if the obstacle side has a cluster tile, and the
# walkable side doesn't. Stops when back at start.
var cluster_corners: Array[Vector2i]
var current_direction: int = start.z
var cx: int = start.x
var cy: int = start.y
var new_direction: int
# Steps off the starting corner, otherwise the loop below would stop
# immediately.
cx += DIR_DX[current_direction]
cy += DIR_DY[current_direction]
# Remove start edge from unvisited.
unvisited.erase(start)
for step in 10_000:
var right_turn = (current_direction + 1) % 4
var straight = current_direction
var left_turn = (current_direction + 3) % 4
var u_turn = (current_direction + 2) % 4
# Decide new direction
if _is_boundary_edge(cx, cy, right_turn, cluster_index):
new_direction = right_turn
elif _is_boundary_edge(cx, cy, straight, cluster_index):
new_direction = straight
elif _is_boundary_edge(cx, cy, left_turn, cluster_index):
new_direction = left_turn
else:
new_direction = u_turn
# Remove current edge from unvisited
unvisited.erase(Vector3i(cx, cy, new_direction))
# If the direction changed, this corner is a vertex
if current_direction != new_direction:
# Calculates the corner position as the margin offsets on both axis of a corner.
var push_x: int = sign(NORMAL_DX[current_direction] + NORMAL_DX[new_direction])
var push_y: int = sign(NORMAL_DY[current_direction] + NORMAL_DY[new_direction])
# Calculates the corners to world space.
var world_x: int = cx * FixedPoint.SCALE + push_x * OBSTACLE_MARGIN
var world_y: int = cy * FixedPoint.SCALE + push_y * OBSTACLE_MARGIN
cluster_corners.append(Vector2i(world_x, world_y))
current_direction = new_direction
# Check if we're back at start
if cx == start[0] and cy == start[1] and current_direction == start[2]:
break
# Move to the next corner
cx += DIR_DX[current_direction]
cy += DIR_DY[current_direction]
all_loops.append(cluster_corners)
return all_loops
## Checks if an edge at corner (cx, cy) facing the given direction is a boundary
## of the specified cluster. An edge is a boundary when the obstacle side (right)
## belongs to the cluster and the walkable side (left) does not.
func _is_boundary_edge(cx: int, cy: int, direction: int, cluster_index: int) -> bool:
# Gets the tile position of the tile to the right (Of walk direction).
var obstacle_tile: Vector2i = Vector2i(cx + CW_OBS_DX[direction], cy + CW_OBS_DY[direction])
# Gets the tile position of the tile to the left (Of walk direction).
var walk_tile: Vector2i = Vector2i(cx + CW_WALK_DX[direction], cy + CW_WALK_DY[direction])
# If the right tile IS in this cluster and the left tile is NOT, then we found an edge.
return obstacle_lookup.get(obstacle_tile, -1) == cluster_index and obstacle_lookup.get(walk_tile, -1) != cluster_index
## Collects all boundary edges of a cluster into a set for tracing.
## Each edge is stored as Vector3i(corner_x, corner_y, direction) where the
## corner and direction define the start of a clockwise boundary edge.
## An edge is a boundary when its obstacle side belongs to this cluster
## and its walkable side does not.
func _get_cluster_boundary_edges(cluster: Array[Vector2i], cluster_index: int) -> Dictionary[Vector3i, bool]:
var boundary_edges: Dictionary[Vector3i, bool] = {}
for tile in cluster:
# Top
if _is_boundary_edge(tile.x, tile.y, DIR_RIGHT, cluster_index):
boundary_edges.get_or_add(Vector3i(tile.x, tile.y, DIR_RIGHT), true)
# Right
if _is_boundary_edge(tile.x + 1, tile.y, DIR_DOWN, cluster_index):
boundary_edges.get_or_add(Vector3i(tile.x + 1, tile.y, DIR_DOWN), true)
# Bottom
if _is_boundary_edge(tile.x + 1, tile.y + 1, DIR_LEFT, cluster_index):
boundary_edges.get_or_add(Vector3i(tile.x + 1, tile.y + 1, DIR_LEFT), true)
# Left
if _is_boundary_edge(tile.x, tile.y + 1, DIR_UP, cluster_index):
boundary_edges.get_or_add(Vector3i(tile.x, tile.y + 1, DIR_UP), true)
return boundary_edges
#endregion
fixed_geometry.gd
class_name FixedGeometry
extends RefCounted
## Computes the 2D cross product of two direction vectors.
## Returns a positive value if vector_b is to the left of vector_a,
## a negative value if vector_b is to the right of vector_a,
## or zero if the vectors are parallel.
## The result is scaled by FixedPoint.SCALE (not SCALE², which is corrected internally).
static func cross_2d(first: FixedVec2, second: FixedVec2) -> int:
@warning_ignore("integer_division")
return (first.x.value * second.y.value - first.y.value * second.x.value) / FixedPoint.SCALE
## Tests whether two line segments cross each other.
## Takes the start and end points of both segments.
## Returns an IntersectionResult with the crossing point and how far along the
## first segment it occurs, or null if the segments do not cross.
## Uses integer-only math — no division is performed for the intersection check,
## preserving full fixed-point precision.
static func segment_intersect(first_start: FixedVec2, first_end: FixedVec2, second_start: FixedVec2, second_end: FixedVec2) -> IntersectionResult:
# Direction vector of the first segment (which way it goes and how long it is).
var first_direction: FixedVec2 = first_end.subtract(first_start)
# Direction vector of the second segment.
var second_direction: FixedVec2 = second_end.subtract(second_start)
# The offset from the start of the first segment to the start of the second.
var gap: FixedVec2 = second_start.subtract(first_start)
# Cross product of the two directions. This is the shared denominator used
# to calculate where along each segment the crossing occurs.
# If zero, the segments point in the same or opposite directions (parallel)
# and can never cross.
var denominator: int = cross_2d(first_direction, second_direction)
if denominator == 0:
return null
# t represents how far along the first segment the crossing occurs.
# t = 0 means at first_start, t = 1 means at first_end.
# We store only the numerator here to avoid dividing (t = t_numerator / denominator).
var t_numerator: int = cross_2d(gap, second_direction)
# u represents how far along the second segment the crossing occurs.
# Same idea: u = 0 means at second_start, u = 1 means at second_end.
var u_numerator: int = cross_2d(gap, first_direction)
# To check if t and u are between 0 and 1 without dividing, we compare
# the numerator against 0 and the denominator. This only works cleanly
# when the denominator is positive, so we flip all signs if it's negative.
if denominator < 0:
denominator = -denominator
t_numerator = -t_numerator
u_numerator = -u_numerator
# If t is outside 0–1, the crossing falls beyond the first segment's endpoints.
if t_numerator < 0 or t_numerator > denominator:
return null
# If u is outside 0–1, the crossing falls beyond the second segment's endpoints.
if u_numerator < 0 or u_numerator > denominator:
return null
# Compute the intersection point: first_start + (t_numerator / denominator) * first_direction.
# Multiply before dividing to preserve precision in integer math.
@warning_ignore("integer_division")
var point_x: int = first_start.x.value + (first_direction.x.value * t_numerator) / denominator
@warning_ignore("integer_division")
var point_y: int = first_start.y.value + (first_direction.y.value * t_numerator) / denominator
var point: FixedVec2 = FixedVec2.from_fixed_point(FixedPoint.from_raw(point_x), FixedPoint.from_raw(point_y))
return IntersectionResult.new(t_numerator, denominator, point)
fixed_vec2.gd
## Deterministic 2D vector using FixedPoint components.
## Used for all simulation positions, velocities, and directions.
## Wraps two FixedPoint values (x, y) and provides vector math
## operations like add, subtract, and distance.
class_name FixedVec2
extends RefCounted
## The X value of the [FixedVec2]
var x: FixedPoint
## The Y value of the [FixedVec2]
var y: FixedPoint
## Creates a new [FixedVec2] from two integer values.
static func from_int(int_x: int, int_y: int) -> FixedVec2:
var result = FixedVec2.new()
result.x = FixedPoint.from_int(int_x)
result.y = FixedPoint.from_int(int_y)
return result
## Creates a [FixedVec2] from two existing [FixedPoint] values.
static func from_fixed_point(fp_x: FixedPoint, fp_y: FixedPoint) -> FixedVec2:
var result = FixedVec2.new()
result.x = fp_x
result.y = fp_y
return result
## Creates a [FixedVec2] from two already-scaled integer value.
## Use when you've calculated the internal value yourself.
static func from_raw(raw_x: int, raw_y: int) -> FixedVec2:
var result = FixedVec2.new()
result.x = FixedPoint.from_raw(raw_x)
result.y = FixedPoint.from_raw(raw_y)
return result
## Adds another [FixedVec2] to this one and returns the result.
func add(other: FixedVec2) -> FixedVec2:
var result = FixedVec2.new()
result.x = x.add(other.x)
result.y = y.add(other.y)
return result
## Subtracts another [FixedVec2] from this one and returns the result.
func subtract(other: FixedVec2) -> FixedVec2:
var result = FixedVec2.new()
result.x = x.subtract(other.x)
result.y = y.subtract(other.y)
return result
## Converts to Godot's [Vector2] for rendering. Not for simulation use.
func to_vector2() -> Vector2:
var result = Vector2.ZERO
result.x = x.to_float()
result.y = y.to_float()
return result
intersection_result.gd
## Result of a line segment intersection test.
## Returned by FixedGeometry.segment_intersect when two segments cross.
## A null return means no intersection occurred.
class_name IntersectionResult
extends RefCounted
## How far along the first segment the intersection occurs (numerator part).
## Compare two hits by cross-multiplying: hit_a.t_numerator * hit_b.t_denominator
## vs hit_b.t_numerator * hit_a.t_denominator, avoiding division.
var t_numerator: int
## How far along the first segment the intersection occurs (denominator part).
var t_denominator: int
## The exact position where the two segments cross.
var intersection_point: FixedVec2
func _init(t_numerator_value: int, t_denominator_value: int, intersection_point_value: FixedVec2) -> void:
t_numerator = t_numerator_value
t_denominator = t_denominator_value
intersection_point = intersection_point_value
raycast_result.gd
## Result of a ray cast against obstacle boundary polygons.
## Returned by Pathfinder when a ray from A to B hits a boundary edge.
## Contains the intersection details plus which polygon and edge were hit,
## so the edge-walker knows where to start navigating around the obstacle.
class_name RaycastResult
extends RefCounted
## The intersection point, t value, and related data from the segment test.
var intersection: IntersectionResult
## Index into obstacle_boundaries identifying which polygon was hit.
var boundary_index: int
## Index of the first vertex of the hit edge within that polygon.
var edge_index: int
func _init(intersection_value: IntersectionResult, boundary_index_value: int, edge_index_value: int) -> void:
intersection = intersection_value
boundary_index = boundary_index_value
edge_index = edge_index_value
![]() ,
,