How to rotate an object around a point

actuallykron · May 21, 2024, 3:46pm

Godot Version

4.2.stable

Question

I’m trying to make a movement system where an object rotates around a point. The point position is set by clicking with the mouse.

I’ve got it mostly working but as the object is rotating it slowly gets further and further away from the point. (video example below)

Does anyone know why this is happening and how to fix it?

My code:

extends CharacterBody2D

var speed : float = 100.0
var click_pos : Vector2 = Vector2(0,0)

func _physics_process(delta: float) -> void:
	handle_movement(delta)

func handle_movement(delta) -> void:

	# set click pos 
	if Input.is_action_just_pressed("left_click"):
		click_pos = get_global_mouse_position()
	
	# movement
	var angle = get_angle_to(click_pos)
	velocity = Vector2(0, 1).rotated(angle)
	var collision_info = move_and_collide(velocity * delta * speed)

	# bounce
	if collision_info:
		velocity = velocity.bounce(collision_info.get_normal())

Sweatix · May 21, 2024, 8:22pm

This is an innate problem of how computers simulate systems of motion.

Systems of motion can be thought of as the integration of an entity’s state. As an example, acceleration affects velocity which affects position.

Acceleration → Velocity → Position

Simulation (no external forces)

In simulations where an entity is not affected by external forces (such as gravitational acceleration or collision impulses), the position of the entity is derived solely from the starting velocity (commonly referred to as v0). This is the case because acceleration is not a factor, so velocity never changes i.e. the velocity will always be what it was when the object started moving.

Because of this, tick-rate (the update rate in one second) does not matter. The accumulation of positional changes (the integration of the system) always evaluates to the same number.

Mathematical example

Taking the following equation

p = p0 + v0 * dt
p: position
p0: starting position
v0: starting velocity
dt: delta time

…it can easily be shown that differing update rates do not matter when simulating a length of time.

State values (dependent variables)

p0 = (0, 0)
v0 = (1, 2)

Delta time of 1.0 (one tick)

dt = 1.0
p = p0 + v0 * dt

= (1, 2)

Delta time of 0.25 (four ticks)

dt = 0.25
p = p0 + (v0 * dt) * 4
= (1, 2)

In such a system, the entity either:

Moves linearly in one direction forever
Never moves

Simulation with changing external forces

If we assume that the external forces of the simulation are constant, the simulation still does not dependent on tick-rate. A common example is gravity which, for all intents and purposes, remains constant. As such, the effect of gravity on the state of the entity can be calculated using calculus - no computers and tick-rates required.

The problem comes when wanting to calculate the state of the entity when external forces vary over time: collision forces, constraints and so on. The state of the system can no longer be reliably calculated via calculus because the forces in the system are, in simple terms, unknown over time.

This is why simulations run in ticks (a.k.a. steps); the state of the system is updated and the next state is computed based on this state. In theory, the result of these numerical simulations approach the true solution. However, you would need an impossibly high tick-rate for the simulation in order to produce such results - tick-rates so high that they can no longer run in real-time.

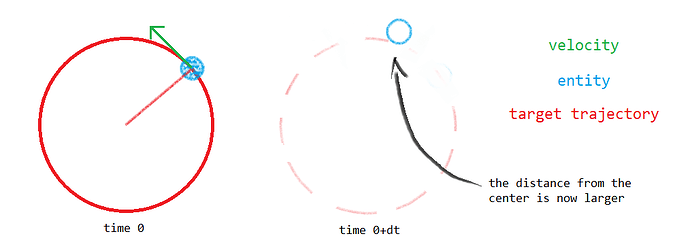
Your problem

As seen in the illustration above, performing numerical simulation will inevitably make your entity stray from the target trajectory. To solve this problem, you have to take this fact into account.

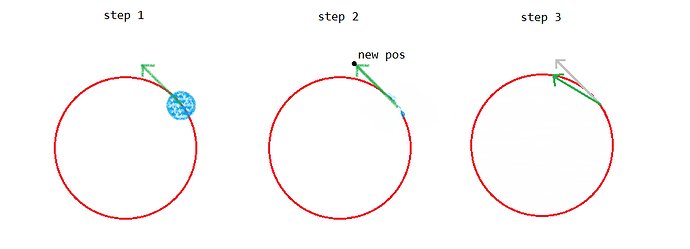
Solution

Compute your new velocity based of off the vector between your click_point and your object position (like you’re already doing)
Compute the next position, new_pos, and limit its distance from the click_point
Compute the vector between this limited new_pos and your entity’s position. This will be your velocity.

If you have any questions, or the approach doesn’t work, please let me know.

actuallykron · May 22, 2024, 12:42am

Thanks for your very detailed reply and especially for including the illustrations (they helped a lot).

I think I understand the concept of the solution but I’m not very good at this stuff so I’m having trouble actually implementing it.

1 - I assume I’m doing this part right (based on what you said above) but from here I’m pretty much lost.

2 - How would I calculate the next position in code and then limit the distance from the click position? And how do I work out how much I should limit it by?

3 - Would this be something along the lines of velocity = (entity_pos - new_pos)?

Thanks!

Sweatix · May 22, 2024, 2:11am

Step 2

We want the distance offset of the next position to be the same as it is currently - otherwise the radius of the trajectory will grow as you’re currently experiencing. You’re essentially trying to determine where on the imaginary (red) circle the new position lies.

Here’s an example

# The middle of your red circle
var click_pos = get_global_mouse_position()

# The velocity that is tangent to the point on the circle
var new_velocity = Vector2(0, 1).rotated(angle)  # This is your code

# This is the next position (without modification)
# This would be further away from the click_pos than your current position
# ...we don't want that
var new_pos = global_position + new_velocity

# Get the vector pointing from the current position
# ...to the circle center (click_pos)
var to_center = click_pos - global_position
# Get the direction to the new position (new_pos)
# ...and multiply by the current distance to the circle center
var pos_on_circle = (new_pos - click_pos).normalized() * to_center.length()

# The point is now the same distance away from
# ...the center as your current position is
# ...so the new position (pos_on_circle) is now implicitly on the circle

Step 3

Assuming that you’re substituting entity_pos for global_position here, you’re almost correct. The vector should point towards the point on the circle, not towards the entity.
Remember that whenever you calculate a vector between two points, the equation will always look like

vector = end - start
In your case:
velocity = new_pos - entity_pos

In other words, the first point in the equation will always be the end of the vector (where the arrow is).

If we resume from the code in step 2, the missing code should look something like this

# The velocity is simply the vector between the point on the circle
# ...and the current position (the green arrow in step 3)
var corrected_velocity = pos_on_circle - global_position

# Apply the new, corrected velocity to the character body
velocity = corrected_velocity

I hope this helps you understand the calculations as well as the reasoning for them.

actuallykron · May 22, 2024, 6:07pm

Once again, thanks for the extremely detailed and well explained reply!

Using your example I was able to get it working correctly. The only thing I had to do was add click_pos to the pos_on_circle calculations to offset it.

For anyone curious, here is the code I’m using:

extends CharacterBody2D

@export var max_speed = 0.0
var speed : float = 0.0
var click_pos : Vector2 = Vector2(0, 0)
var to_center : Vector2 = Vector2(0, 0)
var pos_on_circle : Vector2 = Vector2(0, 0)

func _physics_process(delta: float) -> void:
	if Input.is_action_just_pressed("left_click"):
		click_pos = get_global_mouse_position()
		to_center = (click_pos - global_position)
		speed = max_speed
	
	handle_movement(delta)

func handle_movement(delta):

	var angle = get_angle_to(click_pos)
	var new_velocity = Vector2(0, -1).rotated(angle) 

	var new_pos = (global_position + new_velocity)
	pos_on_circle = ((new_pos - click_pos).normalized() * to_center.length()) + click_pos
	
	var corrected_velocity = pos_on_circle - global_position
	velocity = corrected_velocity

	move_and_collide(velocity * speed * delta)

Not sure if this is completely relevant to this post but I’ll ask it here anyway. The above code works great until the speed variable is set to a value above 120.

For some reason setting it to any higher value will make it go crazy (video example below). I’m honestly so confused to as why this is happening and why 120 is the limit as it’s seemingly a random number. Sorry to keep bothering you about this topic, but would you happen to know why this happens and/or how to fix it? Thank you for your helpful answers so far, I really appreciate it!

Sweatix · May 22, 2024, 7:44pm

Hmm…
Actually, it’s better to use the displacement/offset instead of the velocity for the constraint computation.

I imagine that your artefact/bug is caused by the velocity vector “extending past” the trajectory circle. The constraint is currently trying to correct the velocity based on how far the entity moves in one second (velocity is in m/s). It should actually be based on the offset produced by the velocity:

offset = velocity * speed * delta
Code: move_and_collide(velocity * speed * delta)

After having another look at your code, I also missed the fact that the speed is multiplied at the end instead of the beginning. The speed (i.e. the length of the velocity vector) is paramount to constraining the motion correctly; otherwise the entity will overshoot the pos_on_circle that we’re targeting as the speed was not accounted for when computing said position.

This is a direction: Vector2(0, -1).rotated(angle)
This is a velocity: Vector2(0, -1).rotated(angle) * speed

This is my bad. I gave a long description of how computers simulate dynamic systems – and then I forget about it when making the example…

Here’s your code corrected with the above considerations in mind:

func handle_movement(delta):

	var angle = get_angle_to(click_pos)
	var new_velocity = Vector2(0, -1).rotated(angle) * speed

	# The change in position caused by the velocity (in one frame/tick/update)
	var offset = new_velocity * delta

	var new_pos = (global_position + offset)
	pos_on_circle = ((new_pos - click_pos).normalized() * to_center.length()) + click_pos

	# OLD CODE
	#var corrected_velocity = pos_on_circle - global_position
	#velocity = corrected_velocity
	#move_and_collide(velocity * speed * delta)

	# NEW CODE
	var corrected_offset = pos_on_circle - global_position
	move_and_collide(corrected_offset)

	# NOTE: I opted to not use the velocity-variable as you're not using move_and_slide()
	#       If you later choose to use move_and_slide(), you have to derive the velocity
	#       from the offset like so: velocity = corrected_offset * (1.0/delta)

Hopefully this completely solves your issue(s).

actuallykron · May 24, 2024, 1:23pm

Thank you once again! Everything is now working correctly. I really appreciate your help!

Sweatix · May 24, 2024, 4:01pm

Fantastic!

If the latest code snippet is the best solution, please mark that reply as the actual solution. Others that may look at this post in the future will often only look at whatever is marked as the solution.

system · June 23, 2024, 4:02pm

This topic was automatically closed 30 days after the last reply. New replies are no longer allowed.